Problem Statement

Given an m x n integer matrix heightMap representing the height of each unit cell in a 2D elevation map, return the volume of water it can trap after raining.

Example 1:

Input: heightMap = [[1,4,3,1,3,2],[3,2,1,3,2,4],[2,3,3,2,3,1]]
Output: 4
Explanation: After the rain, water is trapped between the blocks.
We have two small pounds 1 and 3 units trapped.
The total volume of water trapped is 4.

Example 2:

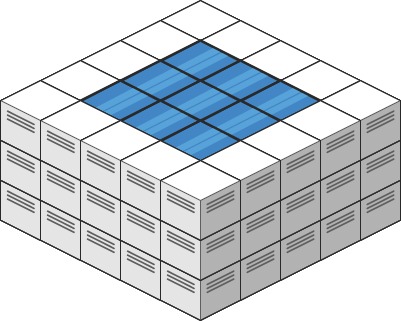
Input: heightMap = [[3,3,3,3,3],[3,2,2,2,3],[3,2,1,2,3],[3,2,2,2,3],[3,3,3,3,3]]
Output: 10

Constraints:

• m == heightMap.length
• n == heightMap[i].length
• 1 <= m, n <= 200
• 0 <= heightMap[i][j] <= 2 * 104

Problem Link

Trapping Rain Water II - LeetCode

Reference Video

https://www.youtube.com/watch?v=QvQiQcLCQ4Y&ab_channel=CherryCoding[IIT-G]

Code

typedef pair<int,pair<int,int>> ppp;
class Solution {
public:
    int trapRainWater(vector<vector<int>>& heightMap) {
        
        int m = heightMap.size();
        int n = heightMap[0].size();
        
        priority_queue<ppp,vector<ppp>,greater<ppp>> pq;
        vector<vector<bool>> visited(m,vector<bool>(n,false));
        
        //Pushing boundry heights into the min heap
        for(int i=0;i<m;i++)
        {
            for(int j=0;j<n;j++)
            {
                if(i==0||j==0||i==m-1||j==n-1)
                {
                    pq.push({heightMap[i][j],{i,j}});
                    visited[i][j] = true;
                }
            }
        }
        
        int vol = 0;
        int minBdHt = 0;//minumum boundry height
        vector<int> dx{0,0,-1,1};
        vector<int> dy{1,-1,0,0};
        
        while(!pq.empty())
        {
            auto p = pq.top();
            int ht = p.first;
            int i = p.second.first;
            int j = p.second.second;
            pq.pop();
            
            minBdHt = max(minBdHt,ht);
           
            for(int k=0;k<4;k++)
            {
                int ni = i+dx[k];
                int nj = j+dy[k];
                
                if(ni<0||nj<0||ni>m-1||nj>n-1||visited[ni][nj])
                    continue;
                
                visited[ni][nj] = true;
                pq.push({heightMap[ni][nj],{ni,nj}});
                
                if(heightMap[ni][nj]<minBdHt)
                {
                    vol+=(minBdHt-heightMap[ni][nj]);
                   
                   
                }
                
            }
            
            
        }
        
        return vol;
        
        
        
    }
};