Alice and Bob take turns playing a game, with Alice starting first.
Initially, there are n stones in a pile. On each player's turn, that player makes a move consisting of removing any non-zero square number of stones in the pile.
Also, if a player cannot make a move, he/she loses the game.
Given a positive integer n, return true if and only if Alice wins the game otherwise return false, assuming both players play optimally.
Example 1:
Input: n = 1
Output: true
Explanation:Alice can remove 1 stone winning the game because Bob doesn't have any moves.
Example 2:
Input: n = 2
Output: false
Explanation:Alice can only remove 1 stone, after that Bob removes the last one winning the game (2 -> 1 -> 0).
Example 3:
Input: n = 4
Output: true
Explanation: n is already a perfect square, Alice can win with one move, removing 4 stones (4 -> 0).
Constraints:
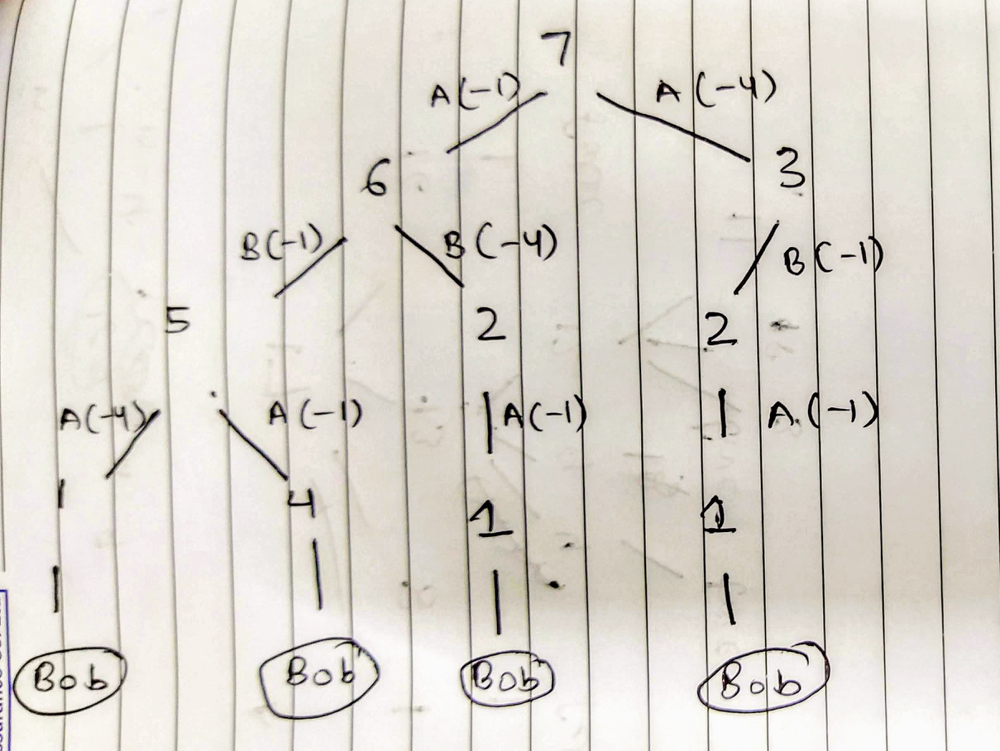
1 <= n <= 105Let's enumerate all possible moves for n = 7:

As you can see, for Alice, there is no subtree that can make him win.
Now let's consider for n = 8. Can Alice choose a subtree that can make him win?