Problem Statement

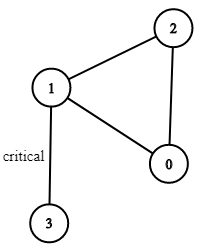
There are n servers numbered from 0 to n-1 connected by undirected server-to-server connections forming a network where connections[i] = [a, b] represents a connection between servers a and b. Any server can reach any other server directly or indirectly through the network.

A critical connection is a connection that, if removed, will make some server unable to reach some other server.

Return all critical connections in the network in any order.

Example 1:

Input: n = 4, connections = [[0,1],[1,2],[2,0],[1,3]]
Output: [[1,3]]
Explanation: [[3,1]] is also accepted.

Problem Link

Critical Connections in a Network - LeetCode

Reference Videos

https://www.youtube.com/watch?v=ZeDNSeilf-Y&list=PLEJXowNB4kPzByLnnFYNSCoqtFz0VKLk5&index=28&ab_channel=TECHDOSE

https://www.youtube.com/watch?v=Rhxs4k6DyMM&list=PLEJXowNB4kPzByLnnFYNSCoqtFz0VKLk5&index=29&ab_channel=TECHDOSE

https://www.youtube.com/watch?v=HsBefuOqkd4&ab_channel=TECHDOSE

Code

class Solution {
public:
    
    
    vector<vector<int>> criticalConnections(int n, vector<vector<int>>& connections) {
         vector<int> adj[n];
        
        for(int i=0;i<connections.size();i++)
        {
            adj[connections[i][0]].push_back(connections[i][1]);
            adj[connections[i][1]].push_back(connections[i][0]);
            
        }
        vector<vector<int>> bridges;
        
        tarjans(n,bridges,adj);
        
        return bridges;
    }
    void tarjans(int n, vector<vector<int>>&bridges,vector<int>adj[])
    {
        vector<int> dis(n,-1); //discovery times of vertices
        vector<int> low(n,-1); //node with lowest discovery time accessible, 
// its values changes when the dfs call returns
        vector<int> parent(n,-1);//if node v comes after node u through an edge {u,v} 
// then u is called the parent of v. here in the entire algorithm we do not consider the
// edges{v,u} i.e from child to parent
        
        for(int i=0;i<n;i++)
        {
            if(dis[i]==-1)
                dfs(i,n,bridges,adj,dis,low,parent);
        }
    }
    void dfs(int u,int n,vector<vector<int>> &bridges,vector<int>adj[],vector<int> &dis,vector<int> &low,vector<int> &parent)
    {
        static int time = 0;
        dis[u] = time; //value of discovery time of u, remains constant throughout the course of algorithm 
        low[u] = time; //initial value of low[u], may change during the course of algorithm
        time++;
        
        for(int v:adj[u])
        {
            if(dis[v]==-1)
            {
                parent[v] = u;
                dfs(v,n,bridges,adj,dis,low,parent);
                //when the dfs call for vertex v in the edge{u,v} ends update the low[u]
                low[u] = min(low[u],low[v]); //if edge {u,v} is not a back edge
                
                if(dis[u]<low[v])
                    bridges.push_back(vector<int>({u,v}));
            }
            else if(v!=parent[u])//Ifa new child v is visited 
                // for which dis[v]!=-1 and v is not the parent of u 
                // then the edge {u,v} is a backedge, which can never be a cut edge 
                low[u] = min(low[u],dis[v]);//if edge {u,v} is a back edge
        }
    }
};