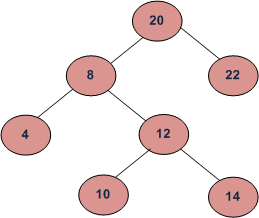
Given a Binary Search Tree, find median of it. If no. of nodes are even: then median = ((n/2th node + (n+1)/2th node) /2 If no. of nodes are odd : then median = (n+1)/2th node.For example, median of below BST is 12.

More Examples:
Given BST(with odd no. of nodes) is :
6
/ \\
3 8
/ \\ / \\
1 4 7 9
Inorder of Given BST will be : 1, 3, 4, 6, 7, 8, 9
So, here median will 6.
Given BST(with even no. of nodes) is :
6
/ \\
3 8
/ \\ /
1 4 7
Inorder of Given BST will be : 1, 3, 4, 6, 7, 8
So, here median will (4+6)/2 = 5.
Asked in: Google
Median of a BST in O(1) space for coding interview round
Find median of BST in O(n) time and O(1) space - GeeksforGeeks
https://www.youtube.com/watch?v=BuI-EULsz0Y&ab_channel=FitCoder
/*
Time Complexity: O(N)
Space Complexity: O(1)
Where 'N' is the total number of nodes of the BST.
*/
int size(TreeNode<int>* root)
{
int nodes = 0;
TreeNode<int>* currNode = root;
TreeNode<int>* prev;
while(currNode != NULL)
{
if(currNode -> left == NULL)
{
nodes += 1;
currNode = currNode -> right;
}
else
{
prev = currNode -> left;
// Finding the inorder predecessor to currNode.
while(prev -> right != NULL && prev -> right != currNode)
{
prev = prev -> right;
}
if(prev -> right == NULL)
{
prev -> right = currNode;
currNode = currNode -> left;
}
else
{
prev -> right = NULL;
nodes += 1;
currNode = currNode -> right;
}
}
}
return nodes;
}
int medianBST(TreeNode<int>* root)
{
TreeNode<int>* temp = root;
int nodes=size(temp);
TreeNode<int>* currNode = root;
TreeNode<int>* prev;
// Previous denotes the predecessor node to currNode.
TreeNode<int>* previous;
int currCount = 0;
while(currNode != NULL)
{
if(currNode -> left == NULL)
{
currCount += 1;
// The odd case.
if(nodes%2 != 0 && currCount == (nodes + 1) / 2)
{
return currNode -> data;
}
// The even case.
if(nodes%2 == 0 && currCount == (nodes / 2 + 1))
{
return (previous -> data + currNode -> data) / 2;
}
previous = currNode;
currNode = currNode -> right;
}
else
{
prev = currNode -> left;
// Finding the inorder predecessor to currNode.
while(prev -> right != NULL and prev -> right != currNode)
{
prev = prev -> right;
}
if(prev -> right == NULL)
{
prev -> right = currNode;
currNode = currNode -> left;
}
else
{
prev -> right = NULL;
previous = prev;
currCount += 1;
// The odd case.
if(nodes%2 != 0 && currCount == (nodes + 1) / 2)
{
return currNode -> data;
}
// The even case.
if(nodes % 2 == 0 && currCount==(nodes / 2 + 1))
{
return (previous -> data + currNode -> data) / 2;
}
previous = currNode;
currNode = currNode -> right;
}
}
}
}